正答率0.2％485人中1人。

すごい問題ですね。
これはひらめきと発見が大事です。
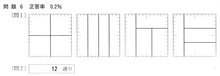
この問題の趣旨は、例題の3つに分ける、次の問1、4つに分ける。
この問題の出し方からつながりの発想を求めていると推察できます。
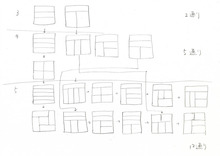
上の解答の2枚目（自作）。
要は流れなのです。
結婚し子どもが出来、孫が生まれの発想。
細かな計算等必要なし。問1でマスに12刻みがあるせいでどつぼにはまった人もいるでしょう。
ただ問1にヒントがあるんですよ。
普通に考えれば12×12で144。割る4で一つ36。
この組み合わせは、3×12、4×9、6×6。
始めはこれで表を作りました。でも中に8×4.5という少数が入ってきます。
ここで気がつきました。
小学生の問題です。思考大会です。つながりで解くのではないか？
そこで計算後回しに解答2枚目の様に考え始めました。細かな数字等後でどうでも出来ます。

解答２枚目に関して。
例題から３個に分けるのは２通り。
問１から４個に分けるのは５通り。
この事から、
解答２枚目の
一番左の列。２つのパターンで２通り。
次に
左から２個目の正方形の「上に横にのびる１個を固定したとすると」
残りの部分で４個作らなければならない。
なのでここで５通り。
次に下の行左から２個目では、
「正方形の上に横にのびる２個を固定したとすると」
後の部分で３個作らなければならない。
例題により２通り。
次に同様に下の行左から４番目では、
「正方形の上に横にのびる３個を固定したとすると」
１通り。
あとの２通りはひらめく事が出来るか？
一番上のマスを半分に割って２個とすると
残りで３個。３個出来るのは２通りしか無いので
２通り。
結果、２通り＋５通り＋２通り＋１通り＋２通りで１２通り。

正解した1人はどんな人なのでしょう？
もしかしたら同様の問題を過去にした事があるのかもしれません。でなければかなりのあたまやわらか少年ですね。